No antigo Egito e na Babilonia, região onde hoje se localiza o Iraque, encontramos as primeiras sistematizações. Foi na Grécia, contudo, durante o grande desenvolvimento da cultura clássica, que se observou o mais significativo desenvolvimento da trigonometria.
Hiparco de Nicea, por volta de 150 anos a.C. e Claudio Ptolomeu, entre os anos 90 e 150 d.C., são considerados os fundadores da Trigonometria. Ambos eram astrônomos, e preocupavam-se com a compreensão do posicionamento das estrêlas e com a elucidação dos movimentos dos principais astros. A Hiparco deve-se, por exemplo, a construção das primeiras tabelas trigonometricas e a divisão da circunferência em 360 partes iguaiscada uma delas denominada 'grau", além do primeiro instrumento de medição de ângulo e da invenção do astrolábio esférico.Talvez por isso seja chamado por muitos historiadores de " pai da Astronomia ".
Uma das grandes conquistas que contribuiram para as navegações e para a evolução da conpreensão do movimentos dos astros foi a possibilidade de determinar distâncias astronômicas e de calcular a paralaxe dos astros e estrêlas tomados como referenciais para os navegadores ou mesmo na medida de distâncias importantes para o estabelecimento dos primeiros mapas.
Chama-se paralaxe ao deslocamento aparente de um objeto devido ao deslocamento do observador.
O método mais comum para se medir grandes distâncias ou pontos inacessíveis é a triangulação.
Suponha por exemplo, que seja necessário saber a medida da distância de uma árvore localizada do outro lado de um rio que não podemos atravessar.
Observe o triangulo ABC formado pela árvore no vértice A, e pelos pontos distintos de observação B e C.
podemos construir um triângulo BED semelhante a ABC traçando, convenientemente uma paralela ao lado AC . Se desejamos calcular por exemplo AC, a semelhança dos dois triangulos nos dará
AC = (BC. DE) / BE
Observe que AC é uma distância impossível de ser medida, pois BC, BE, EC estão na mesma margem do rio. No caso da árvore, a paralaxe é indicada pela diferença das direções de observação dos pontos B e C
Para calcular a distância da terra a um astro, os astrônomos utilizam basicamente o mesmo método que utilizamos para a árvore, ou seja, baseavam-se no conceito de paralaxe.
Utilizando o processo de cálculo das paralaxes e tomando como referência determinadas estrelas cujas distância aproximada da Terra já havia sido calculada, os cartógrafos conseguiam determinar grandes distâncias na superfície do planeta.
Razões Trigonométricas no triângulo retângulo
Os triangulos ABC, ADE, AFG são semelhantes
Portanto
seus lados correspondentes são proporcionais ou seja:
BC/AC = DE/AE = FG/AG.
Na segunda figura temos (a) para cateto oposto do ângulo Â
(c) para adjacente do ângulo A e
(b) para hipotenusa. Daí vem :
Sen  = BC/AC ou Sen  =DE/AE ou Sen Â=FG/AG
No segundo caso ainda da segunda figura temos c= cateto adjacente portanto o Cos= c/b
Cateto adjacente / hitpotenusa
E ainda temos a Tangente = cateto oposto / cateto adjacente
Num triangulo retangulo onde a=6 b=10 c=8
Sen Â= 6/10 ou 3/5
Cos Â=8/10 ou 4/5.
Tg  = 6/8 ou 3/4
30° 45° e 60° 30° sen=0,500 cos=0,866 tg = 0,577
45° 0,707 0,707 1,000
60° 0,866 0,500 1,732
Calcular o valor de X
 =45º a=X b=20 a =cateto oposto b= hipotenusa
Sen  = a/b 0,707 = X/ 20 X= 0,707x20 = 14,14
Determinar o cos.
Â= 40° x cateto adjacente b=hipotenusa = 10
Cos de 40° =0,766 Cos 40°= x/10 x= 10.Cos 40° x=10 . 0,766 ou x=7,66
CIRCUNFERÊNCIA TRIGONOMÉTRICA
ARCOS -
Chamamos de ARCO DE CIRCUNFERÊNCIA AB cada uma das partes em que a circunferência fica dividida por dois de seus pontos
ÂNGULO CENTRAL
É todo ângulo cujo vértice coincide com o centro da circunferência e cujos lados são raios dessa circunferência.
OBS- A medida do ângulo central é igual a medida do arco de circunferência.
COMPRIMENTO DE UMA CIRCUNFERÊNCIA
Consideremos uma circunferência de raio r
Cortando a circunferê4ncia e esticando a linha que a representa, obtemos um segmento AB
A medida do segmento AB representa o comprimento da circunferência e é dado por
C= 2r.(pi)
UNIDADES PARA MEDIR ARCOS
GRAU
Um GRAU é definido como a medida do ângulo central submetido por um arco igual a 1/360 da circunferência que contém o arco. Indica-se 1°
Um MINUTO é igual a 1/60 do grau. (Indica-se 1´ )
Um SEGUNDO é igual a 1/60 do minuto ( indica-se 1´´ )
Então podemos dizer que um arco de uma volta mede 360°
RADIANO
O RADIANO ( simbolo rad ) é definido como a medida de um ângulo central submetido por um arco igual ao raio da circunferência que contém o arco.
Como a medida de uma circunferência ( ou arco de uma volta ) mede 2 (pi) rad .ou 360° podemos estabelecer entre as unidades as relações
360° = 2(pi)rad ou 180° = (pi) rad.
Exemplo:
Expressar 300° em rad 180° (pi) rad
300° X 180/300 = (pi)/ x
x= 5(pi)rad / 3
Simples regra de 3.
Exemplo - Expressar 22° 3O´ em rad
Resolução
Vamos transformar 22° 30´ em minutos
22° . 60` + 30 = 1350 minutos
transformando 180° em minutos + 10 800´ armando uma regra de 3 temos x=(pi)/8 rad.
Expressar em graus
10 (pi)/3 rad 10 . 180 : 3 x= 600°
(pi)/4 em graus 180 : 4 = 45°
O COMPRIMENTO DE UM ARCO DE CIRCUNFERÊNCIA
S= comprimento do arco m= medida do ângulo central r= raio
obs- a medida do ângulo central ( rad)
S= m .r
Exemplo - Numa circunferência de raio = 30 cm, qual é o comprimento de um arco que subtende um ângulo central de 60°
m=60° = 180/3 rad r=30cm
S = 10 (pi ) cm S = 10 . 3,14 = 31,4 cm.
CIRCUNFERÊNCIA TRIGONOMÉTRICA ou CICLO TRIGONOMÉTRICO
Figura a) A sentido ante horário B ( positivo )
Figura b) sentido horário A para B ( negativo )
Figura D) 0° - 0 rad - Arcos congruos - Um angulo de 1 volta = 360°
90°- 1/2 rad Se tivermos um angulo de 500°: 360°=1 volta e
180°- 1 rad sobra 140° então
270°-3/2 rad o ângulo de 500° graus é congruo de 140°
360°-2 rad. Quando a medida do angulo é dada em radianos, convertemos essa medida para graus e só aí procederemos como no ex. anterior.
N° trigonometrico - Seno ( sen) de um arco
localiza-se na ordenada 0 y e chama-se sen de X
OBS- nos quadrantes temos Seno 0°=0 Sen 90° =1 Sen 180° =0 Seno 270°=-1
Cos 0° =1 cos 90° =0 cos de 180°= -1 Cos 270°=0
O cosseno ( cos) de um arco localiza-se na abscissa 0X e chama-se cos de X
Nota_ o arco de 360° ou 2 rad é congruo do arco 0° logo Sen 360° = Sen de 0° = 0
Cos de 360°=cos de 0° = 1
VARIAÇÂO DO SINAL
Sen x e cos x no I quadrante são positivos No III quadrante sen e cos são negativos
No II quadrante sen positivo e cos negativo
No IV quadrante Sen negativo
Cos positivo
O sen de 30° =1/2 cos 30/ raiz de 3 : 2
O sen de 60°= raiz de 3:2 o cos de 60° é = 1/2
O sen de 45° = raiz de 2 :2 o cos de 45° é = Raiz de 2 : 2
RELAÇÕES FUNDAMENTAIS
sen²x + cos² x = 1
Tangente de um arco = sen x : cos x
Cotangente de um arco = cos x : sen x
cossecante x = 1 : sen x
secante = 1 : cos x
RELAÇÕES DERIVADAS
sec² x= 1+ tg²x
cossec²x+ 1 + cotg²
REDUÇÃO AO 1° QUADRANTE
Se x é um arco do 2° quadrante, então (180-x) será um arco do 1° quadrante.
Arco do 3° quadrante então (x-180) será um arco do 1° quadrante
Arcos do 4° quadrante então (360° - x) será um arco do 1° quadrante.
TRANSFORMAÇÕES TRIGONOMETRICAS
Fómulas da adição
Sejam a e b dois arcos positivos, do 1° quadrante, cuja soma ainda pertence ao 1° quadrante:
Valem para esses arcos as seguintes identidades:
ADIÇÃO E SUBTRAÇÃO DE ARCOS
Sen (a+b) = sen a . cos b+ sen b . cos a
Sen (a-b) = sen a . cos b - sen b . cos a
Cos ( a+b ) = cos a . cos b - sen a. sen b
cos ( a-b ) = cos a - cos b + sen a . sen b
tg ( a+b ) = ( tg a + tg b ) : (1 - tgt a . tg b)
tg ( a- b) =( tg a - tgb ) : ( 1 + tg a . tgb )
CONSEQUÊNCIAS DAS FORMULAS DE ADIÇÂO
cos 2a = cos² a - sen² a
tg 2a = ( 2 tg a :: ( 1 - tg² a )
FÓRMULAS DA TRANSFORMAÇÃO EM PRODUTO
sen m + sen n = 2 sen (m+n) : 2 . cos (m-n) : 2
sen m - sen n = 2 . sen (m-n) :2 . cos ( m+n ) : 2
EQUAÇÔES TRIGONOMÉTRICAS
Toda equação em que figura uma função trigonométrica , com arco descomhecido, recebe o nome de equação trigonométrica
Assim são equações trigonométricas:
sen x = 0
sen x = 1/2
2sen x - cosec x = 1
cos ( 2x - Pi/2 ) = 1
Sen x . tgx + 2 cos x = 2
sen 2x + 1 = 0
Chama-se solução de uma equação trigonométrica os valores da variável , caso existiam, que satisfazem a equação dada.
RESOLUÇÃO DE UMA EQUAÇÃO DA FORMA
sen x = m, com -1< m < 1
ex. Resolver a equação sen x =1 , com 0< x<2 pi
Resolução
1=sen pi/2 OBS não esquecer que (pi) em trigonometria = 180°
e (pi) em geometria = 3,14...
daí sen x =1
1=sen (pi/2 )
portanto a solução da equação é pi/2 S= { pi/2 }
RESOLVER A SEGUINTE EQUAÇÃO TRIGONOMÉTRICA COM AUXÍLIO DE UMA DAS EQUAÇÕES TRIGONOMÉTRICAS DADAS
2 sen² x -5 sen x +3 = 0, com 0< x <2pi
Esta equação é de 2º grau em sen x
a= 2
b= -5
c= 3 delta = 1 x, =3/2 x,, =1
x, não convém porque pois -1 < sen x < 1
O valor que satisfaz é 1 = x,, sen x =1
1= sen pi/2 portanto a solução é PI/2
INEQUAÇÕES TRIGONOMÉTRICAS
Resolver a inequação sen x > 0 para 0 < x < 2 pi Observando a figura vemos que a solução da inequação é S= { x / 0 < x< pi }
 .
.Vamos estudar a variação da FUNÇÃO sen x com x variando no intervalço [ 0, 2pi] sempre no sentido anti- horário, neste exemplo
O gráfico da função seno é chamado de senóide.
O gráfico continua à direita de 2 pi e à esquerda de 0 ( zero).
A função seno é positiva para valores de 1º e 2º quadrantes e é negativa para valores de 3º e 4º quadrantes.
No 1º quadrante: x cresce de 0 a 2/pi seno x cresce de 0 a 1
No 2º quadrante x cresce de pi/2 a pí seno x decresce de 1 a 0
No 3º quadrante x cresce de pi a 3 pi/2 seno x decresce de 0 a -1
No 4º quadrante x cresce de 3pi/2 a 2 pi seno x cresce de 0 a -1
O dominio da função seno x é o conjunto dos números reais, isto é, D =R
A imagem da função seno x é o intervalo [ -1,+1], isto é , -1 < seno x < 1 ( menor ou igual )
Resolvendo um problema
Determinar K para que exista O ARCO QUE SATISFAÇA A IGUALDADE
SEN X = 2K - 5
Resolução - devemos ter -1 < ou = sen x < ou = 1 substituindo temos:
-1 < 2k -5 < 1 ( obs < ou =)
-1 +5<2k <1+5
4 <2k<6
2 < k<3 Resposta S= { x que pertence R/ 2 < K < 3}
PERÍODICIDADE da função do seno
Observando a sinuosidade do seno em seu gráfico notamos que a partir de 2pi a função seno repete seus valores
As funções que repetem seus valôres são chamadas FUNÇÕES PERIÓDICAS ; portanto a função do seno é periódica. e nesse caso p = 2pi.
(P = período)
Construir o gráfico dafunção y =2sen x, dando o domínio, a imagem eo período
Resolução
Tabelando a função temos
x sen x 2 sen x y
0 0 2.0 0
pi/2 1 2.1 2
pi 0 2.0 0
3pi/2 -1 2.(-1) -2
2pi 0 2.0 0
Estudo do Co-seno
Definição
Consideremos o ciclo trigonométrico no qual marcaremkos o ponto M que é a imagem , no ciclo do niumero real x e seja OM, a abscissa do ponto M em relação ao plano cartesiano.
Conclusão - Dado um arco AM , de medida x radianos, definimos como coseno x a abscissa do ponto M e representamos cos x = OM
Definimos função coseno como função f que associe a cada número real OM = mcos x e indicamos f(x) = cos x ou y = cos x
Problemas - Calcular o valor de cos 1830°
1830 : 360° = 5 com sobra de 30°
Então 1830° = 30° + 5.360°
Cos de 1830 ° = cos de 30° = Raiz de 3 : 2
Calcular o valor do cos 13 pi
13pi/2pi = 13/2 + 1/2 = 6 + 1/2
13 pi = ( 1/2 + 6 ) 2pi = pi +6 . 2 pi
Então cos 13 pi = cos pi = 1
Gráfico
A cosenoide, continua à direita de 2 pi e a esquerda de 0 ( zero)
Observando o gráfico temos :
A função coseno é positiva para valores do 1° e 4° quadrantes e é negativa para os valores 2º
e 3° quadrantes.
No 1° quadrante x cresce de 0 a pi/2 - cos x decresce de 1 a 0
No 2° quadrante x cresce de pi/2 a pi - cos x decresce de 0 a -1
No 3° quadrante x cresce de pi a 3pi/2 - cos x cresce de -1 a 0
No 4° quadrante x cresce de 3pi/2 a 2pi - cos x cresce de 0 a 1
O domínio da função cos x é o conjunto dos numeros reais, isto é, D=R
A imagem da função cos x é o intervalo [ -1,1] , isto é -1 < ou = cosx<ou = +1.
Exemplo - Determinar K de modo que se tenha cos x = 3K +4
Devemos ter : -1 <ou = cos x <ou = 1 ( vou usar < no lugar de <ou= só para não escrever ou=)
-1 < 3K +4 <1
-1-4<3K < 1-4
-5 < 3K <-3
-5/3 < K < -1 S= { K E R / -5/3< K<-1 }
<ou=
Tabelando uma função:
x cox 3cos x y Exemplo: ( Construir o gráfico y= 3 cos x dar dominio, imagem e periodo)
0 1 3.1 3
pi/2 0 3.0 0
pi - 1 3.-1 -3
3pi/2 0 3.0 0 o gráfico formará uma cosenoide iniciando em +3 descendo ao 0 em (pi/2) a
2pi 1 3.1 3 -3 em ( pi ) a zero em ( 3/2pi ) e a +3 em ( 2pi)
D=R Im= [-3.3 ] P= 2pi
.
ESTUDO DA FUNÇÃO DA TANGENTE
Definição-Na figura ( 1 ) Consideremos o ciclo trigonometrico no qual marcamos o ponto M que é a imagem , no ciclo, do número real x e seja T a intersecção da reta OM com o eixo t das tangentes.
Vemos que o ponto T não existe quando M = B ou M = B' e que a medida do segmento AT é função de x, isto é, a cada x diferente de pi/2 + K( pi ) corresponde um único número AT.
Então
a) Dado um arco AM , de medida x radianos , com x diferente Pi/2 + kPi, definimos como tangente de x a medida algébrica do segmento AT e representamos tg x = AT ( x diferente pi/2 + k pi )
b) Definimos função tangente como a função f que associa a cada número real x ( com x diferente pi/2 + kpi ) o número real AT = tg x e indicamos f(x) = tg x ou y=tg x.
Vamos observar agora a figura -2
triangulo OAT semelhante ao triangulo OMM¹
AT/MM¹ = OA/OM¹
AT/Sen x = 1/ Cos x
AT= sen x/ cos x
Então podemos dizer que :
Função tangente é a função f que associa a cada número real x ( com x diferente pi/2 + kipi ) o número real AT = tg x = sen x/ cos x
obs- a restrição x diferente de pi/2 + kpi é para excluir os valores de x para os quais cos x = 0 )
Observação importante :
Fig 3 - Esta nova definição tem a vantagem de ser aplicada de uma forma mais completa PORQUE AGORA PODEMOS FALAR EM TANGENTES DE ANGULOS MAIORES DE 90° OU 360°
E ATÉ DE ANGULOS COM MEDIDAS NEGATIVAS.
Observe agora, usando a definição
tg 0° = sen 0°/ cos 0°= 0/1 = 0
tg 90°= tg pi/2 = sen pi/2 dividido por cos pi/2 = 1/0 ( não é definida )
tg 180° tg pi = sen pi / cos pi = 0/-1 = 0
tg 270° = tg 3pi / 2 = sen 3pi/2 dividido por cos 3pi /2 = -1/0 ( não é definida )
tg 360° = tg 2pi = sen 2pi dividido por cos 2 pi = 1/0 = 0
outros valores já vistos anteriormente como tg 30° raiz de 3 dividido por 3
de 45° =1 , de 60° = raiz de 3 ...
Observe os seguintes exemplos:
determinar o valor da tangente de 1845°
1845: 360 = 5 e sobram 45° então 1845° = 45° + 5 . 360°
Determinar o valor de tg 10 pi
10pi/2pi= 5 10pi= (5) . 2pi = 0 + 5 . 2pi
Então tg 10 pi = tg 0 =0
Estudo da variação no gráfico
Vamos estudar a variação da função tg x com x variando no intervalo [ 0,2pi], isto é , o ponto M parte do ponto A e se movimenta sobre o ciclo no sentido anti- horário.
O gráfico da função tangente é chamado tangentóide
O gráfico da função tangente continua à direita de 2pi e à esquerda de 0 (zero)
A função tangente é positiva para valores do 1º e 3º quadrantes e é negativa para valores do 2º e 4º quadrantes.
No primeiro quadrante : x cresce de zero a pi/2 tg x cresce de 0 a + infinito
No 2º quadrante x cresce de pi/2 a pi : tg x cresce de - infinito a zero
No 3º quadrante x cresce de pi a 3/2 pi : tg x cresce de zero a + infinito
4º quadrante x cresce de 3/2pi a 2 pi : tg x cresce de - infinito a zero.
O dominio da função x é D= { x pertence a R / x é diferente de pi/2 + K (pi) com K Pertencente a Z
A imagem da funçãqo tg x é o intervalo ] - infinito , + infinito[ , isto é - infinito < tg x< + infinito.
Periodicidade é ( pi )
O bserve que de pi em pi a função tangente repete seus valores portanto o período da função tangente é pi ( p = pi )
TRIANGULOS QUAISQUER :
Para desenvolver o estudo sobre as relações trigonométricas num triangulo qualquer é importante rever como se classificam os triangulos quanto as medidas dos lados e dos angulos
Quanto aos lados, o triangulo pode ser:
equilátero ( se os tres lados tiverem a mesma medida ou medidas iguais).
isosceles ( se dois lados tiverem medidas iguais)
escaleno ( se os tres lados tiverem medidas diferentes )
Quanto aos angulos, os triangulos podem ser
acutangulo ( se tiver os tres angulos agudos)
Retangulo ( se tiver um angulo reto )
obtusangulo ( se tiver um angulo obtuso )
TEOREMA DOS SENOS, DOS COSSENOS E DA ÀREA DE UM TRIANGULO QUALQUER
Vamos considerar um triangulo , não retangulo, qualquer, ABC
a/ sen  = b/ sen ^B = c/ sen C
A área de qualquer triangulo ABC pode ser assim determinada:
Sabemos que a área = 1/2 a.h (I)
Considerando o tri8angulo AHC temos
Sen ^C = h/b h= b. sen ^C (II)
Das relações ( I) e (II) temos o teorema da área
Àrea = 1/2 a.b.sern ^C
De forma análogo podemos fazer de um triangulo de lados a,b,c que
Àrea = 1/2 b.c sen Â
Àrea = 1/2 a.c.sen ^B.
Embora a demonstração tenha sido feita num triangulo acutangulo , ela também pode ser verificada nos triangulos obtusangulo e retangulo.
SAIBA UM POUCO MAIS
O LUGAR DA TERRA ( Fonte : História do Pensamento , NOVA CULTURAL )
Por muitos séculos a Terra ocupou o lugar central no Universo. Sabemos que essa hipótese ultrapassada alimentou deusesw, e vários preconceitos que impediram a ciencia , durante séculos de caminhar.
" A maldição era a pena sofrida por quem tentasse retirar a Terra dessa posição."
No século III a.C. Aristarco de Samus , matemático e astrônomo, fez essa tentativa, aliás mal sucedida.
Sòmente 18 séculos depois, Nicolau Copérnico ( 1473 -1543) conseguiu, postumamente faze-lo.
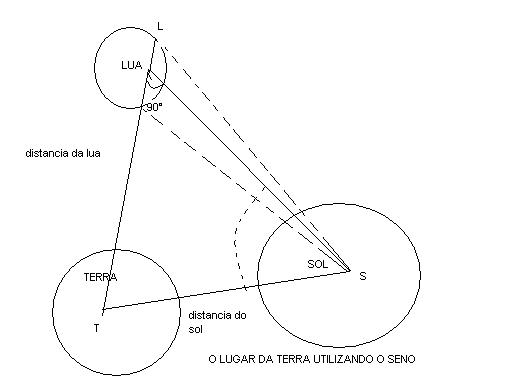
Um dos estudos feitos por Aristarco foi sobre a distância entre a Terra eo Sol.Considerando as condições da época, foi de grande engenhosidade o cáculo feito por ele. Em suas observações, percebeu que o centro da Lua , em quarto crescente, o centro do Sol e um observador na Terra representam 3 pontos que se forem ligados , formam um triangulo retângulo SLT
Seus cálculos levaram-no a concluir que a distância da Terra ao Sol (TS) é 18 a 20 vezes a distância da Terra à Lua ( TL ).
Cálculo esse que, embora perfeito, necessita do conhecimento sobre S E N O S
Sen x = TL / TS ou
1/ sen x = TS /TL
Para que 1 / sen x assuma um valor entre 18 e 20 Aristarco utilizou para o ângulo de medida x o complementar de ^T , ou seja 3°
1 / sen 3° = 19,11
Embora a distância esteja correta, o ângulo ^S é diferente dos 3° adotados, o seu valor efetivo é 10'. Para isso, deve ter contribuído a precariedade de instrumentos .
Exemplo :
1º Reduzir ao 1º quadrante o arco de 2/3 pi radianos.Considera-se o arco pi - 2/3 pi =pi/3
E temos Seno 2/3pi = seno pi/3 cos 2/3pi= - cos pi/3 tg 2pi/3 = - tg pi/3
As demais linhas é fácil de calcular .
2ºReduzir ao 1º quadrante o arco 210°
Considera-se o arco de 210° - 180°= 30°
. Temos seno 210° = -seno 30° cos 210° = - cos 3o° tg 210° = tg 30°
3º Reduzir ao 1º quadrante o arco 320 grados.
Considera-se o arco de 400 gr - 320gr = 80 gr. temos portanto temos seno 320 gr - - seno 80 gr cos 320 gr = cos 80 gr e tg 320gr = - tg 80 gr.
4º Reduzir ao 1º quadrante o arco de 930
Toma-se o arco congruo de 930 menor do que 360°, que é 210, pois 930° = 2 X 360° + 210°
E procede-se como no 2º exemplo
Seno 930° = seno de 210° = - seno de 30°
cos 930 ° = cos 210° = - cos 30°
tg 930° = tg 210° = tg 30°
EXERCÍCIOS RESOLVIDOS :
1- Calcular o valor numérico da expressão:
y= cos 4x + seno 2x + tg 2x- sec 8x para x = pi/2
portanto y = cos 2x + seno pi + tg pi - sec 4pi = 1 + 0 + 0 - 1 = 0
2- Reduza ao 1º quadrante cosec 480° ( ESCOLA NAVAL -1952 )
Dividindo 480° por 360° = 1 e resto 120. Então 480° = 1 x 360 + 120
portanto cosec 480° = cosec 120° = cosec ( 180 - 120 ) = cosec 60°
3- Simplificar a expressão : Y = numerador tg( pi/2 + x) cos ( 3pi/2 - x ) cos - ( -x) sobre
denominador cot( x+ x ) seno (3pi/2 + x )
(Obs) Y = (uma fração ) simplificando a expressão já que se trata de uma fração sobra Y = - seno x
Cáculo das linhas trigonométricas dos arcos expressos pela relação pi/n
TEOREMA - O seno de um arco positivo, menor do que meio pi radiano, é igual a metade da corda que submete o arco duplo . Seja um circulo trigonométrico de centro O e AM¹ = a um arco desse circulo. Tracemos a corda M¹ M"" perpendicular ao diametro A A' Como todo diâmetro perpendicular a uma corda divide esta corda ao meio, então M'P = M""P.
Sendo AM' um arco = seno a = M1P = M1M""/2
e como M1 M"" é a corda que subntende o arco duplo 2a, então está demonstrado o teorema
CÁLCULO DAS LINHAS TRIGONOMÉTRICAS DOS ARCOS pi/n.
Para calcular as linhas trigonométricas de um arco pi/n basta calcular o seno deste arco de acordo com o teorema anterior. Temos que o seno pi/n é a metade da corda do arco duplo 2pi/n, mas, a corda do arco duplo é o lado do polígono regular de n lados inscrito num círculo. E#ntãoseno pi/n = Ln/2 conhecendo o seno é fácil conhecer as demais funções.
APLICAÇÕES;
1º - FUNÇÕES TRIGONOMÉTRICAS do arco de 30°.
SENO 30° = seno pi/6 = R/2 = 1/2
portanto cos de 30° = Raiz quadrada de 1-1/4 = V3 / 2 = e tangente 30° = V3/3
2º -FUNÇÕES TRIGONOMÉTRICAS do arco de 45°
sen 45° = sen pi/4 = L4/2 = R V2/ 2e tg 45° = 1
3º- FUNÇÕES TRIGONOMÉTRICAS do arco de 60°
seno 60° = seno pi/3 = L3/2 =RV3/2 = V3/2
cos 60° = Raiz quadrada de (1-3/4) = 1/2 e tg 60° = V3
EXERCÌCIOS RESOLVIDOS
1º - Calcular a fração de denominador racional que é igual a co secante do arco pi/12, sabendo-se que o lado do dodecágono regular inscrito no círculo trigonométrico é (V6 - V2) / 2
sen pi/12 = L12/ 2 = (V6 - V2) / 4 maqs , cosec pi/12 =4/ (V6 - V2 )
portanto cosec pi/12= 4 ( V6 + V2)/ ( 6-2) = V6 + V2
2º - Calcular o seno 690°
Reduzindo ao 1º quadrante seno 690 = seno 360 = - seno 30° = - 1/2
3º - Calcular y = 4 V3 . tg 150° + 3 seno 90° .tg 225° - 6 seno 330° + cos 270°
y= 4V3 X( - tg 30°) + 3X 1 X ( tg 45°) - 6 ( - seno 30°) + 0 = 2